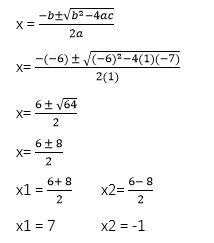Solve the equation
(a) 4x2 -25 = 0 (c)
X2 – 6x + 9 = 0
(b) x2 – 6x – 7 = 0 (d) 3X2 + 5x – 2 = 0
Answer
COMPLICATED
|
EASY
|
(a) 4x2
-25 = 0
2X +5
2X -5
So (2X
+5)(2X-5) = 0
2X+5 = 0 2X – 5 = 0
X = -5/2 X = 5/2
|
Use
Calculator only
First
Press MODE > EQN > DEGREE (2) Then insert the value a, b and c.
1. MODE,
2. EQN, 3. DEGREE (2), for a press 4, then press =, for b press 0 then press
= and for c press -25 and press =
You will
get the answer X1 = 2.5 which is equal to 5/2 and X2= -2.5 or -5/2
So X = 5/2 and X = -5/2
X = 5/2 X = -5/2
2X = 5 2X = -5
2X-5 = 0 2X + 5 = 0
(2X-5)(2X+5)
= 0
X = -5/2,
5/2#
|
(b) x2
– 6x – 7 = 0
X -7
X +1
(X-7)(X+1)
= 0
X -7 =
0 X +1= 0
X = 7 X = -1
|
1. MODE,
2. EQN, 3. DEGREE (2), 4. a press 1 then press =, 5. b press -6 then press =,
6. c press -7 then =
The answer
will be
X1 = 7, X2
= -1
|
(c) X2
– 6x + 9 = 0
X -3
X -3
(X-3)(X-3)
= 0
X-3 = 0
X = 3
|
a = 1, b =
-6 c =9
X=3
|
(d) 3X2
+ 5x – 2 = 0
3X -1
X +2
(3X-1)(X+2)=
0
3X-1 = 0 X+2 = 0
X = 1/3 X = -2
|
a = 3, b =
5, c = -2
X1 = 1/3,
X2= -2
|
**For additional mathematics it is better for you to calculate it by just using calculator cause it will save your time in examination.
SOLVING BY
COMPLETING THE SQUARE
Example 1:
Solve the equation x2 – 6x -7 = 0 by completing the
square.
Answer:
x2 – 6x -7 = 0
x2 – 6x = 7 (*Transfer the constant to the right side)
x2 – 6x + (-6/2)2 = 7+ (-6/2)2 (*Add
[Coefficient of x/2]2 to the both side)
x2 – 6x + (-3)2 = 7+9
(x-3)2 = 16 (*Completing the square) (*Remove -6x)
x-3 = (16)1/2
x-3 = ± 4
x = 4 + 3 or x = -4 +
3
x = 7 x = -1
*You can check the answer using the calculator whether your answer
is right or wrong using the above step. MODE > EQN > DEGREE (2).
Example 2:
Solve the equation x2 + 2x -3 = 0 by completing the
square.
Answer:
x2 + 2x -3 = 0
x2 + 2x = 3
x2 + 2x + (2/2)2 = 3 + (2/2)2
x2 + 2x + (1)2 = 4
(x + 1)2 = 4
x + 1 = (4)1/2
x + 1 = ± 2
x = 2 -1 or x = -2 -1
x = 1 x = -3
Example 3:
Solve the equation x2 -4x -12 = 0 by completing the
square.
Answer:
x2 - 4x -12 = 0
x2 -4x = 12
x2 -4x + (-4/2)2 = 12 + (-4/2)2
x2 -4x + (-2)2 = 16
(x -2)2 = 16
x – 2 = (16)1/2
x – 2 = ± 4
x = 4 + 2 or
x = -4 + 2
x = 6 x = -2
SOLVING BY USING THE FORMULA
Example 1:
Solve the equation x2 - 6x – 7 = 0 by using formula.
Answer
x2 - 6x – 7 = 0
a = 1, b = -6, c = -7
**If you want to check your answer whether right or not, you just need to key in the number into the calculator, using the above method and you will get the right answer.
Example
2:
Solve the quadratic equation 4x2 - 9x + 1 = 0 by
using formula. Give your answers correct to two decimal places.
Answer
4x2 - 9x + 1 = 0
a= 4, b = -9, c = 1
FORMING QUADRATIC EQUATIONS FROM GIVEN ROOTS
Example
Form a quadratic equation whose roots are
(a) 3 and -4 (b)
5 only (c) 2 and 3
(a) 3 and -4
|
(b) 5 only
|
(c) 2 and 3
|
Since
the roots are 3 and -4, so we can write x = 3 and x = -4.
*You
can use any alphabet whether “x”, “y”, “z”, or others.
x = 3 x = -4
x-3 =
0 x + 4 = 0
(x-3)(x+4) = 0
x2
+ 4x -3x – 12 = 0
x2 + x -12 = 0#
OR
Using
this formula:
x2
– (α + β)x +αβ = 0
*a and
b is root
x2
– (3+(-4))x + (3)(-4) = 0
x2
+ x – 12 = 0
|
x = 5
x-5 =
0
(x-5)(x-5)
= 0
x2 – 10x + 25 = 0#
OR
x2
– (α + β)x +αβ = 0
x2
– (5+5)x + 5(5) = 0
x2
-10x +25 = 0
|
x =
2 x = 3
x-2 =
0 x – 3 =0
(x-2)(x-3)
= 0
x2-5x +6 = 0#
OR
x2
– (α + β)x +αβ = 0
x2
– (2+3)x +2(3) = 0
x2
– 5x + 6 = 0
|
SUM OF ROOTS AND PRODUCT OF ROOTS
Roots α and β
(x - α)(x – β) = 0
x2 –βx - αx+αβ = 0
x2 – (α + β)x +αβ = 0
x2 – (sum of roots)x +(product of roots) = 0
---------------- (1)
lets α and β be also the roots of the quadratic equation
ax2 + bx + c = 0
x2 + bx/a + c/a = 0 ------------- (2)
Therefore:
x2 – (α + β)x +αβ = 0 ---------------- (1)
x2 + bx/a + c/a = 0 ------------- (2)
Sum of roots: α + β
= -b/a
Product of roots: αβ = c/a
Example
1:
Determine the sum and the product of roots for each of the
following quadratic equation.
(a) 3x2 – 6x + 1 = 0 (b)
-x2 – 8x + 5 = 0
(c) x2 –6x+3 =0 (d)
2x2 – 3x - 2 =0
(a) 3x2 – 6x + 1 = 0
|
(b) -x2 –8x +5 =0
|
(c) x2 –6x+3 =0
|
(d) 2x2 – 3x - 2 =0
|
3x2
– 6x + 1 = 0 (*Let x2 be alone by dividing the 3 to others)
x2
– 6x/3 + 1/3 = 0
x2
– 2x + 1/3 = 0
a b
c
SOR: α + β = -b/a
b =
-2, a = 1
= -(-2)/1
= 2
POR:
αβ = c/a
c =
1/3, a = 1
= [1/3]/1
= 1/3
*to
check whether your answer correct of not, you can build the equation by using
the SOR and POR using this formula x2
– (sum of roots)x +(product of roots) = 0. If the equation same with the given
equation so your answer is true.
|
-x2
– 8x + 5 = 0
x2
– 8x/(-1) + 5/(-1) = 0
x2
+ 8x - 5 = 0
SOR: α + β = -b/a
= -8/1
= -8
POR:
αβ = c/a
= -5/1
= -5
|
x2
– 6x + 3 = 0 (*Since the x2 already alone and positive you can
proceed to SOR and POR.
SOR: α + β = -b/a
=
-(-6)/1
= 6
POR:
αβ = c/a
= 3/1
= 3
|
2x2
– 3x - 2 =0
x2
– 3x/2 – 2/2 =0
x2
– 3x/2 –1 =0
SOR: α
+ β = -b/a
=
-(-3)/1
= 3
POR:
αβ = c/a
=
(-1)/1
= -1
|
Example
2:
If α and β are the roots of the equation x2 –6x+3 =0,
form the equations whose roots are
(a) 2α, 2β (b)
α/β, β/α
Answer:
α and β are the roots of the equation x2 –6x+3 =0
So:
SOR: α + β = -b/a POR: αβ = c/a
α + β = -(-6)/1 αβ
= 3/1
α + β = 6 αβ = 3
(a) 2α, 2β
|
(b) α/β, β/α
|
SOR:
2α + 2β
=
2(α+β)
= 2(6)
(*Substitute α + β = 6)
= 12
POR:
(2α)(2β)
= 4 αβ
= 4(3)
(*Substitute αβ = 3)
= 12
Then
form the equation using this formula:
x2
– (SOR)x +(POR) = 0
x2
– (12)x +(12) = 0
x2 – 12x +12 = 0
|
SOR:
α/β + β/α
= [αα
+ ββ]/[αβ]
= [α2
+ β2]/[αβ]
= ([α
+ β]2 - 2αβ)/[αβ]
= ([6]2
– 2[3])/ 3
= [36-6]/3
= 10
POR: (α/β)(β/α)
= αβ/αβ
= 1
x2 – (SOR)x +(POR) = 0
x2 –10x +1 = 0
|
Example
3:
The roots of the equation 2x2 –4x+1 =0 are α and β,
form the equations whose roots are
(a) 3α, 3β (b)
α + 1, β +1 (c) α/β,
β/α
Answer:
α and β are roots of the equation 2x2 –4x+1 =0
2x2 –4x+1 =0
x2 –4x/2 + 1/2 =0
x2 –2x + 1/2 =0
So:
SOR: α + β = -b/a POR: αβ = c/a
α + β = -(-2)/1 αβ
= [1/2]/1
α + β =
2 αβ = 1/2
(a) 3α, 3β
|
(b) α + 1, β +1
|
(c) α/β, β/α
|
SOR: 3α
+ 3β
= 3(α
+ β)
= 3(2)
(Substi: α + β = 2)
= 6
POR: (3α)(3β)
= 9αβ
=
9(1/2)
= 9/2
x2 – (SOR)x +(POR) = 0
x2
–6x +9/2 = 0
2x2 –12x +9 = 0
|
SOR: (α
+ 1) + (β +1)
= (α +
β) + 2
= 2 +
2
= 4
POR: (α
+ 1)(β +1)
= αβ +
α + β + 1
= ½ + 2
+ 1
= 7/2
x2 – (SOR)x +(POR) = 0
x2
–4x +7/2= 0
2x2 –8x +7= 0
|
SOR:
α/β + β/α
= [αα
+ ββ]/[αβ]
= [α2
+ β2]/[αβ]
= ([α
+ β]2 - 2αβ)/[αβ]
= ([2]2
– 2[1/2])/[1/2]
= [4 –
1]/[1/2]
= 6
POR: (α/β)(β/α)
= αβ/αβ
= 1
x2 – (SOR)x +(POR) = 0
x2 – 6x +1 = 0
|
Example
4:
One of the roots of the equation 3x2 – 6x+ k =0 is
three times the other. Find the roots and the value of k.
Answer:
3x2 – 6x+ k =0
x2 – 6x/3 +k/3 =0
x2 – 2x+ k/3 =0
Roots is three times the other
3α and α
SOR: 3α + α = -b/a POR:
3α(α) = c/a
4α = -(-2)/1 3α2 = [k/3]/1
4α = 2 3[1/2]2
= k/3 [Substi: α = ½]
α = ½ ¾
= K/3
k
= 9/4
Since the 3α and α are the roots, α = ½ and 3α = 3/2.
You can check your answer by form an equation based on SOR and POR
3x2 – 6x+ k =0
3x2 – 6x+ 9/4 =0 (Substi: k = 9/4)
12x2 – 24x+ 9 =0
4x2
– 8x+ 3 =0 ------------(1)
x2
– (SOR)x +(POR) = 0
x2 – (2)x +(3/4) = 0
4x2
– 8x +3 = 0 ------------(2)
Equation (1) and (2) are same. So your answer is true.
Example
5:
One of the roots of the equation 2x2 – 8x+ p =0 is two
times the other. Find the roots and the value of p.
Answer:
2x2 – 8x+ p =0
x2 – 8x/2+ p/2 =0
x2 – 4x+ p/2 =0
Roots is three times the other
2α and α
SOR: 2α + α = -b/a POR:
2α(α) = c/a
3α = -(-4)/1 2α2
= [p/2]/1
3α = 4 2α2
= [p/2]
α = 4/3 2[4/3]2
= p/2
32/9 = p/2
p
= 64/9
Since the 2α and α are the roots, α = 4/3 and 2α = 8/3.
You can check your answer by form an equation based on SOR and POR
2x2 – 8x+ p =0
2x2 – 8x+ 64/9 =0 (Substi: p = 64/9)
18x2 – 72x+ 64 =0
18x2 – 72x+ 64 =0
9x2
– 36x+ 32 =0 -----------(1)
x2
– (SOR)x +(POR) = 0
x2 – 4x +32/9 = 0
9x2
– 36x +32 = 0 -------------(2)
Equation (1) and (2) are same. So your answer is true.
Example
6:
If the roots of the x2 + kx + 40 = 0 are in the ratio
2:5, determine the value of k.
ratio 2:5
2α, 5α
SOR: 2α + 5α = -k/1 POR:
2α(5α) = 40/1
7α =
-k 10α2
= 40
α2
= 4
α
= ± 2
7α = -k or
7α = -k
7(2) = -k (Substi: α = 2) 7(-2)
= -k (Substi: α = -2)
k = -14 k
= 14
THE
TYPES OF ROOTS OF A QUADRATIC EQUATION
The
quadratic equation ax2 + bx + c = 0 has
(a)
two roots which are different if b2
– 4ac > 0,
(b)
two roots which are equal if b2 – 4ac = 0,
(c) no
roots if b2
– 4ac < 0
|
Example 1:
Determine the type of roots for each of the following quadratic
equations.
(a) 4x2 -12x + 9 = 0 (b)
3x2 +5x – 2 = 0 (c)
5x2 – 3x + 1 = 0
(d) 2x2 – 3x – 2 = 0 (e)
3x2 - 4x + 5 = 0 (f)
-4x2 + x + 1 = 0
(a) 4x2 -12x + 9 = 0
|
(b) 3x2 +5x – 2 = 0
|
(c) 5x2 – 3x + 1 = 0
|
b2
– 4ac
b =
-12, a = 4, c = 9
(-12)2
– 4(4)(9) = 0
Two
roots which are equal if b2 – 4ac = 0.
So the
equation has two equal roots.
|
b2
– 4ac
b = 5,
a = 3, c = -2
(5)2
– 4(3)(-2) = 49
Two
roots which are different if b2 – 4ac > 0.
So the
equation has two different roots which are different.
|
b2
– 4ac
b =
-3, a = 5, c = 1
(-3)2
– 4(5)(1) = -11
No
roots if b2 – 4ac < 0.
So the
equation does not have any root.
|
(d) 2x2 – 3x – 2 = 0
|
(e) 3x2 - 4x + 5 = 0
|
(f) -4x2 + x + 1 = 0
|
b2
– 4ac
b =
-3, a = 2, c = -2
(-3)2
– 4(2)(-2) = -7
b2
– 4ac < 0
Does
not have any root.
|
b2
– 4ac
b =
-4, a = 3, c = 5
(-4)2
– 4(3)(5) = -44
b2
– 4ac < 0
Does
not have any root.
|
b2
– 4ac
b = 1,
a = -4, c = 1
(1)2
– 4(-4)(1) = 17
b2
– 4ac > 0
Has
two different roots which are different.
|
SOLVING
PROBLEM INVOLVING ‘b2 – 4ac’
Example
1:
Find the value of p if the quadratic x2 – 2px + 2p + 3
= 0 has two equal roots.
Answer:
x2 – 2px + [2p + 3] = 0
a = 1, b = 2p, c = 2p +3
b2 – 4ac = 0 (*Equation has two equal roots)
(2p)2 – 4(1)(2p+3) = 0
4p2 – [8p + 12] = 0
4p2 – 8p -12= 0
p2 – 2p -3 = 0 (*Use calculator [casio 570] to
calculate)
(p + 1)(p – 3) = 0
(p + 1) = 0 or (p – 3) = 0
p = -1 p = 3
Example
2:
Show that the equation kx2 + (1 – 2k)x + k + 3 = 0 has
roots which are different if k < 1/16.
Answer:
a = k, b = 1-2k, c = k + 3
Two roots which are different if b2 – 4ac > 0.
(1- 2k)2 – 4(k)(k+3) > 0
1 – 4k+ 4k2 – 4k(k+3) > 0
1 – 4k+ 4k2 – 4k2 - 12k > 0
1 – 16k > 0 or
-16k > -1
1 > 16k 16k
< 1
1/16 > k k
< 1/16
k < 1/16
Example
3:
Show that the equation (9k-8)x2 – 6kx + k + 2 = 0 has
roots which are different if k < 8/5.
Answer:
a = 9k – 8, b = -6k, c = k + 2
Two roots which are different if b2 – 4ac > 0.
(-6k)2 – 4(9k-8)(k+2) > 0
36k2 – [(36k-32)(k +2)] > 0
36k2 – [36k2 + 72k -32k – 64] > 0
36k2 – [36k2 +40k -64] > 0
-40k + 64 > 0
40k -64 < 0
40k < 64
k < 64/40
k < 8/5
Example
4:
Show that the equation tx2 + (3- 2t)x + t-5 = 0 has no
roots if t < -9/8.
Answer:
a = t, b = 3 – 2t, c = t-5
No roots if b2 – 4ac < 0.
(3-2t)2 – 4(t)(t-5) < 0
9 – 12t + 4t2 - 4t2 + 20t < 0
9 + 8t < 0
8t < -9
t < -9/8